Z2 topological invariant

In this tutorial, we demonstrate the usage of Z2 class by calculating the \(\mathbb{Z}_2\) topological invariant of bilayer bismuth. The corresponding script is located at examples/prim_cell/z2/bismuth.py. We begin with importing the necessary packages:

from math import sqrt, pi

import numpy as np
from numpy.linalg import norm

import tbplas as tb
import tbplas.builder.exceptions as exc

Auxialiary functions

We define the following functions to build bilayer bismuth with SOC:

  1def calc_hop(sk: tb.SK, rij: np.ndarray, label_i: str, label_j: str) -> complex:
  2    """
  3    Evaluate the hopping integral <i,0|H|j,r>.
  4
  5    References:
  6    [1] https://journals.aps.org/prb/abstract/10.1103/PhysRevB.84.075119
  7    [2] https://journals.aps.org/prb/abstract/10.1103/PhysRevB.52.1566
  8    [3] https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.97.236805
  9
 10    :param sk: SK instance
 11    :param rij: displacement vector from orbital i to j in nm
 12    :param label_i: label of orbital i
 13    :param label_j: label of orbital j
 14    :return: hopping integral in eV
 15    """
 16    # Range-dependent slater-Koster parameters from ref. 2
 17    dict1 = {"v_sss": -0.608, "v_sps": 1.320, "v_pps": 1.854, "v_ppp": -0.600}
 18    dict2 = {"v_sss": -0.384, "v_sps": 0.433, "v_pps": 1.396, "v_ppp": -0.344}
 19    dict3 = {"v_sss": 0.0, "v_sps": 0.0, "v_pps": 0.156, "v_ppp": 0.0}
 20    r_norm = norm(rij)
 21    if abs(r_norm - 0.30628728) < 1.0e-5:
 22        data = dict1
 23    elif abs(r_norm - 0.35116131) < 1.0e-5:
 24        data = dict2
 25    else:
 26        data = dict3
 27    lm_i = label_i.split(":")[1]
 28    lm_j = label_j.split(":")[1]
 29    return sk.eval(r=rij, label_i=lm_i, label_j=lm_j,
 30                   v_sss=data["v_sss"], v_sps=data["v_sps"],
 31                   v_pps=data["v_pps"], v_ppp=data["v_ppp"])
 32
 33
 34def make_cell() -> tb.PrimitiveCell:
 35    """
 36    Make bilayer bismuth primitive cell without SOC.
 37
 38    :return: bilayer bismuth primitive cell
 39    """
 40    # Lattice constants from ref. 2
 41    a = 4.5332
 42    c = 11.7967
 43    mu = 0.2341
 44
 45    # Lattice vectors of bulk from ref. 2
 46    a1 = np.array([-0.5*a, -sqrt(3)/6*a, c/3])
 47    a2 = np.array([0.5*a, -sqrt(3)/6*a, c/3])
 48    a3 = np.array([0, sqrt(3)/3*a, c/3])
 49
 50    # Lattice vectors and atomic positions of bilayer from ref. 2 & 3
 51    a1_2d = a2 - a1
 52    a2_2d = a3 - a1
 53    a3_2d = np.array([0, 0, c])
 54    lat_vec = np.array([a1_2d, a2_2d, a3_2d])
 55    atom_position = np.array([[0, 0, 0], [1/3, 1/3, 2*mu-1/3]])
 56
 57    # Create cell and add orbitals with energies from ref. 2
 58    cell = tb.PrimitiveCell(lat_vec, unit=tb.ANG)
 59    atom_label = ("Bi1", "Bi2")
 60    e_s, e_p = -10.906, -0.486
 61    orbital_energy = {"s": e_s, "px": e_p, "py": e_p, "pz": e_p}
 62    for i, pos in enumerate(atom_position):
 63        for orbital, energy in orbital_energy.items():
 64            label = f"{atom_label[i]}:{orbital}"
 65            cell.add_orbital(pos, label=label, energy=energy)
 66
 67    # Add hopping terms
 68    neighbors = tb.find_neighbors(cell, a_max=5, b_max=5, max_distance=0.454)
 69    sk = tb.SK()
 70    for term in neighbors:
 71        i, j = term.pair
 72        label_i = cell.get_orbital(i).label
 73        label_j = cell.get_orbital(j).label
 74        hop = calc_hop(sk, term.rij, label_i, label_j)
 75        cell.add_hopping(term.rn, i, j, hop)
 76    return cell
 77
 78
 79def add_soc(cell: tb.PrimitiveCell) -> tb.PrimitiveCell:
 80    """
 81    Add spin-orbital coupling to the primitive cell.
 82
 83    :param cell: primitive cell to modify
 84    :return: primitive cell with soc
 85    """
 86    # Double the orbitals and hopping terms
 87    cell = tb.merge_prim_cell(cell, cell)
 88
 89    # Add spin notations to the orbitals
 90    num_orb_half = cell.num_orb // 2
 91    num_orb_total = cell.num_orb
 92    for i in range(num_orb_half):
 93        label = cell.get_orbital(i).label
 94        cell.set_orbital(i, label=f"{label}:up")
 95    for i in range(num_orb_half, num_orb_total):
 96        label = cell.get_orbital(i).label
 97        cell.set_orbital(i, label=f"{label}:down")
 98
 99    # Add SOC terms
100    soc_lambda = 1.5  # ref. 2
101    soc = tb.SOC()
102    for i in range(num_orb_total):
103        label_i = cell.get_orbital(i).label.split(":")
104        atom_i, lm_i, spin_i = label_i
105
106        for j in range(i+1, num_orb_total):
107            label_j = cell.get_orbital(j).label.split(":")
108            atom_j, lm_j, spin_j = label_j
109
110            if atom_j == atom_i:
111                soc_intensity = soc.eval(label_i=lm_i, spin_i=spin_i,
112                                         label_j=lm_j, spin_j=spin_j)
113                soc_intensity *= soc_lambda
114                if abs(soc_intensity) >= 1.0e-15:
115                    try:
116                        energy = cell.get_hopping((0, 0, 0), i, j)
117                    except exc.PCHopNotFoundError:
118                        energy = 0.0
119                    energy += soc_intensity
120                    cell.add_hopping((0, 0, 0), i, j, soc_intensity)
121    return cell

Most of them are similar to that of Slater-Koster formulation and Spin-orbital coupling.

Evaluation of Z2

With all the auxiliary functions ready, we now proceed to calculate the \(\mathbb{Z}_2\) invariant number of bilayer bismuth as

 1def main():
 2    # Create cell and add soc
 3    cell = make_cell()
 4    cell = add_soc(cell)
 5
 6    # Evaluate Z2
 7    ka_array = np.linspace(-0.5, 0.5, 200)
 8    kb_array = np.linspace(0.0, 0.5, 200)
 9    kc = 0.0
10    z2 = tb.Z2(cell, num_occ=10)
11    kb_array, phases = z2.calc_phases(ka_array, kb_array, kc)
12
13    # Plot phases
14    vis = tb.Visualizer()
15    vis.plot_phases(kb_array, phases / pi)
16
17
18if __name__ == "__main__":
19    main()

To calculate \(\mathbb{Z}_2`\) we need to sample \(\mathbf{k}_a\) from \(-\frac{1}{2}\mathbf{G}_a\) to \(\frac{1}{2}\mathbf{G}_a\), and \(\mathbf{k}_b\) from \(\mathbf{0}\) to \(\frac{1}{2}\mathbf{G}_b\). Then we create a Z2 instance and its calc_phases function to get the topological phases \(\theta_m^D\). Bilayer bismuth has two Bi atoms, each carrying two \(6s\) and three \(6p\) electrons, totally 10 electrons per primitive cell. So the number of occupied bands is thus 10, as specified by the num_occ argument. After that, we plot \(\theta_m^D\) as the function of \(\mathbf{k}_b\) in the left panel of the figure. It is clear that the crossing number of phases against the reference line is 1, indicating that bilayer bismuth is a topological insulator. We then decrease the SOC intensity \(\lambda`\) to 0.15 eV and re-calculate the phases. The results are shown in the right panel of the figure, where the crossing number is 0, indicating that bilayer bismuth becomes a normal insulator under weak SOC, similar to the case of bilayer Sb.

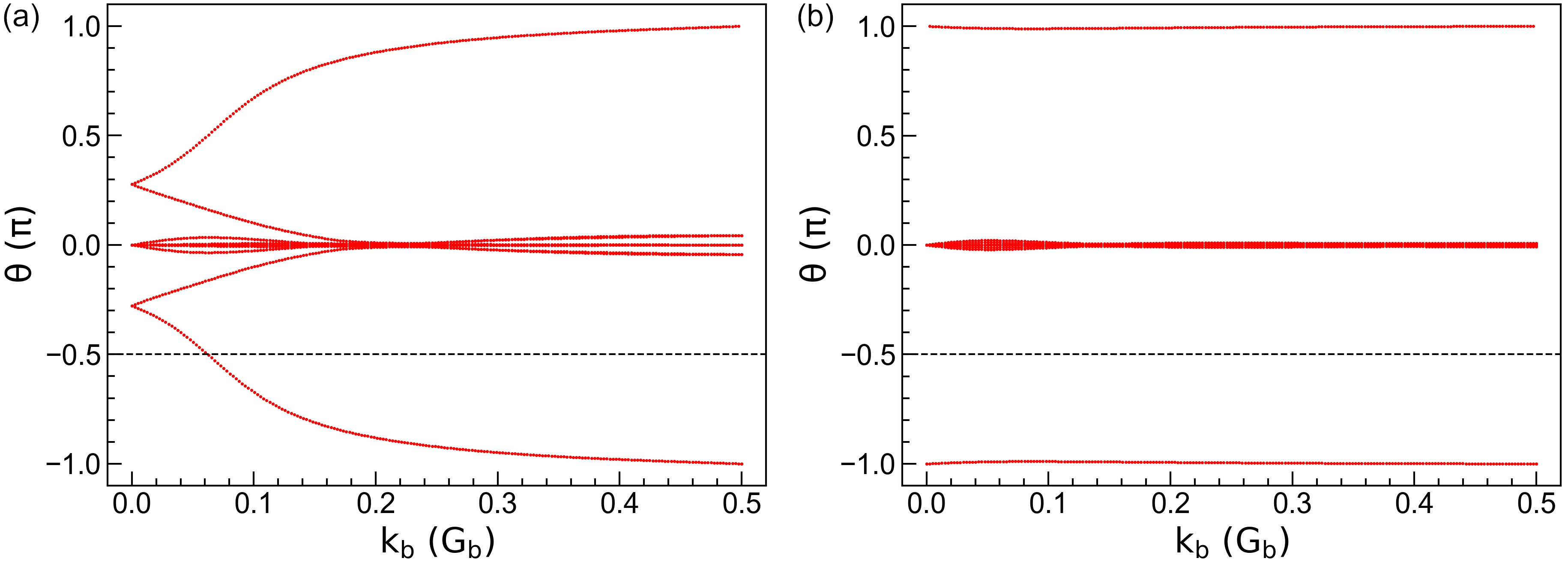
../../_images/bismuth.png

Topological phases \(\theta_m^D\) of bilayer bismuth under SOC intensity of (a) \(\lambda\) = 1.5 eV and (b) \(\lambda\) = 0.15 eV. The horizontal dashed lines indicates the reference lines with which the crossing number is determined.