Spin texture
In this tutorial, we demonstrate the usage of SpinTexture class by calculating the spin
texture and spin-resolved band structure of graphene with Rashba and Kane-Mele spin-orbital coupling.
The spin texture is defined as the the expectation of Pauli operator \(\sigma_i\), which can be
considered as a function of band index \(n\) and \(\mathbf{k}\)-point
where \(i \in {x, y, z}\) are components of the Pauli operator. The spin texture can be evaluated
for given band index \(n\) or fixed energy. The script is located at examples/prim_cell/spin_texture/spin_texture.py.
As in other tutorials, we begin with importing the tbplas package:
from typing import List
import numpy as np
import matplotlib.pyplot as plt
import tbplas as tb
Spin texture
We define the following function for calculating the spin texture:
1def calc_spin_texture(cell: tb.PrimitiveCell,
2 prefix: str = "kane_mele",
3 ib: int = 0,
4 spin_major: bool = True) -> None:
5 # Sigma_z on a fine grid
6 spin_texture = tb.SpinTexture(cell)
7 spin_texture.config.prefix = f"{prefix}_sigma_z"
8 spin_texture.config.k_points = 2 * (tb.gen_kmesh((240, 240, 1)) - 0.5)
9 spin_texture.config.k_points[:, 2] = 0.0
10 spin_texture.config.spin_major = spin_major
11 spin_data = spin_texture.calc_spin_texture()
12 plot_sigma_z_band(spin_data, ib)
13
14 # Sigma_x and sigma_y on a coarse grid
15 spin_texture.config.prefix = f"{prefix}_sigma_xy"
16 spin_texture.config.k_points = 2 * (tb.gen_kmesh((48, 48, 1)) - 0.5)
17 spin_texture.config.k_points[:, 2] = 0.0
18 spin_data = spin_texture.calc_spin_texture()
19 plot_sigma_xy_band(spin_data, ib)
20 plot_sigma_xy_eng(spin_data)
Firstly, we create a SpinTexture object. Then we define the prefix of data files, the k-points
and the order of spin-polarized orbitals. To plot the expectation of \(\sigma_i\) as function of
\(\mathbf k\)-point, we need to generate a uniform mesh grid in the Brillouin zone. As the
gen_kmesh() function generates k-grid on \([0, 1]\), we need to multiply the result by
a factor of 2, then extract 1 from it such that the k-grid will be on \([-1, 1]\) which is enough to
cover the first Brillouin zone. After that, we call the calc_spin_texture method to calculate the spin
texture. The result is a SpinData object, which contains the Cartesian coordinates of k-points,
the energies and the expectation of \(\sigma_x\), \(\sigma_y\) and \(\sigma_z\).
The expectation of \(\sigma_z\) can be visualized as scalar field. We achieve this by calling the
plot_sigma_z_band function. The result is shown in the left panel of Fig. 1. The expectation of
\(\sigma_x\) and \(\sigma_y\) can be visualized simultaneously as vector field. we call the
plot_sigma_xy_band function to visualize \(\sigma_x\) and \(\sigma_y\) of specific band,
and plot_sigma_xy_eng to visualize that of specific energy range. The result is shown in the middle
and right panels of Fig. 1, where the signature of Rashba spin-orbital coupling is clearly demonstrated.
The functions to visualize the results are defined as:
1def plot_sigma_z_band(spin_data: tb.SpinData, ib: int = 0) -> None:
2 """
3 Plot expectation of sigma_z of specific band as scalar field of kx and ky.
4 :param spin_data: spin texture produced of SpinTexture calculator
5 :param ib: band index
6 :return: None
7 """
8 # Data aliases
9 kpt_cart = spin_data.kpt_cart
10 sigma_z = spin_data.sigma_z[:, ib]
11
12 # Plot expectation of sigma_z.
13 vis = tb.Visualizer()
14 vis.plot_scalar(x=kpt_cart[:, 0], y=kpt_cart[:, 1], z=sigma_z, scatter=True,
15 num_grid=(480, 480), cmap="jet", with_colorbar=True)
16
17
18def plot_sigma_xy_band(spin_data: tb.SpinData, ib: int = 0) -> None:
19 """
20 Plot expectation of sigma_x and sigma_y of specific band as vector field of
21 kx and ky.
22 :param spin_data: spin texture produced of SpinTexture calculator
23 :param ib: band index
24 :return: None
25 """
26 # Data aliases
27 kpt_cart = spin_data.kpt_cart
28 sigma_x = spin_data.sigma_x[:, ib]
29 sigma_y = spin_data.sigma_y[:, ib]
30
31 # Plot expectation of sigma_z.
32 vis = tb.Visualizer()
33 # Plot expectation of sigma_x and sigma_y.
34 vis.plot_vector(x=kpt_cart[:, 0], y=kpt_cart[:, 1], u=sigma_x, v=sigma_y,
35 cmap="jet", with_colorbar=True)
36
37
38def plot_sigma_xy_eng(spin_data: tb.SpinData,
39 e_min: float = -2,
40 e_max: float = -1.9) -> None:
41 """
42 Plot expectation of sigma_x and sigma_y of specific energy range as vector
43 field of kx and ky.
44 :param spin_data: spin texture produced of SpinTexture calculator
45 :param e_min: lower bound of energy range in eV
46 :param e_max: upper bound of energy range in eV
47 :return: None
48 """
49 # Data aliases
50 bands = spin_data.bands
51 kpt_cart = spin_data.kpt_cart
52 sigma_x = spin_data.sigma_x
53 sigma_y = spin_data.sigma_y
54
55 # Extract spin texture of specific energy range
56 e_min, e_max = -2, -1.9
57 ik_selected, sigma_x_selected, sigma_y_selected = [], [], []
58 for i_k in range(bands.shape[0]):
59 idx = np.where((bands[i_k] >= e_min)&(bands[i_k] <= e_max))[0]
60 ik_selected.extend([i_k for _ in idx])
61 sigma_x_selected.extend(sigma_x[i_k, idx])
62 sigma_y_selected.extend(sigma_y[i_k, idx])
63
64 # Plot expectation of sigma_x and sigma_y.
65 vis = tb.Visualizer()
66 vis.plot_vector(x=kpt_cart[ik_selected, 0], y=kpt_cart[ik_selected, 1],
67 u=sigma_x_selected, v=sigma_y_selected, cmap="jet",
68 with_colorbar=True)
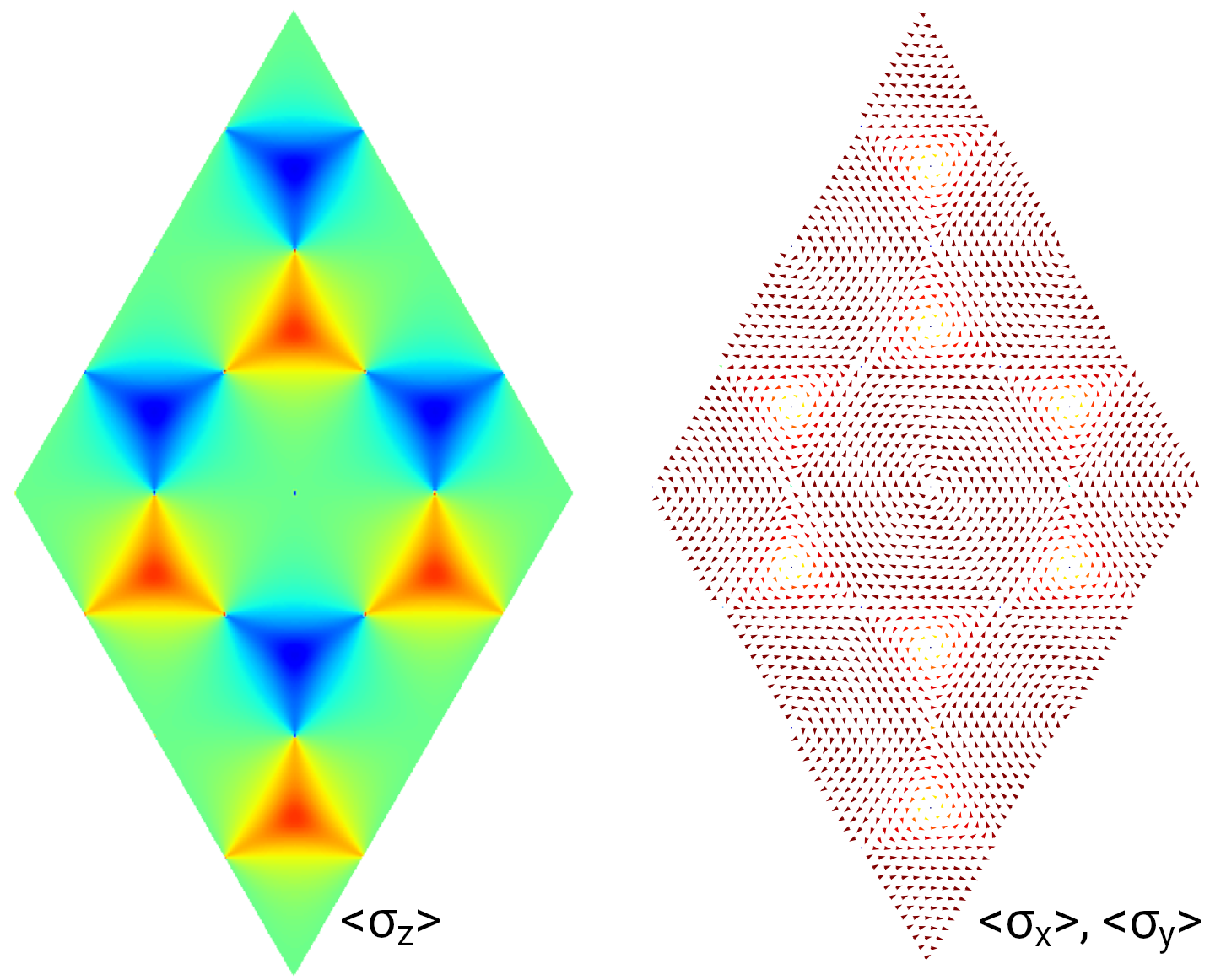
Spin texture of Kane-Mele model. (Left) Expectation of \(\sigma_z\) of 0th band. (Middle) Expectation of \(\sigma_x\) and \(\sigma_y\) of 0th band. (Right) Expectation of \(\sigma_x\) and \(\sigma_y\) of \([-2, -1.9]\) eV.
Spin-resolved band structure
Spin-resolved band structure can be evaluated in the same approach as spin texture. The only difference is that the k-points should be a path connecting high-symmetric k-points in the first Brillouin zone, rather than a regular mesh grid. We define the following function to calculate the spin-resolved band structure:
1def calc_fat_band(cell: tb.PrimitiveCell,
2 prefix: str = "kane_mele",
3 spin_major: bool = True) -> None:
4 # Generate k-path
5 k_points = np.array([
6 [0.0, 0.0, 0.0], # Gamma
7 [0.5, 0.0, 0.0], # M
8 [2./3, 1./3, 0.0], # K
9 [0.0, 0.0, 0.0], # Gamma
10 [1./3, 2./3, 0.0], # K'
11 [0.5, 0.5, 0.0], # M'
12 [0.0, 0.0, 0.0], # Gamma
13 ])
14 k_label = [r"$\Gamma$", "M", "K", r"$\Gamma$",
15 r"$K^{\prime}$", r"$M^{\prime}$", r"$\Gamma$"]
16 k_path, k_idx = tb.gen_kpath(k_points, [40, 40, 40, 40, 40, 40])
17
18 # Evaluate spin texture (including energies)
19 spin_texture = tb.SpinTexture(cell)
20 spin_texture.config.prefix = f"{prefix}_fat_band"
21 spin_texture.config.k_points = k_path
22 spin_texture.config.spin_major = spin_major
23 spin_data = spin_texture.calc_spin_texture()
24
25 # Plot fat band
26 plot_fat_band(spin_data, k_idx, k_label, "z")
The function for visualizing the results is defined as:
1def plot_fat_band(spin_data: tb.SpinData,
2 k_idx: np.ndarray,
3 k_label: List[str],
4 component: str = "z") -> None:
5 """
6 Plot spin-resolved band structure.
7 :param spin_data: spin texture produced of SpinTexture calculator
8 :param k_idx: indices of high-symmetric k-points
9 :param k_label: labels of high-symmetric k-points
10 :param component: component of sigma
11 :return: None
12 """
13 # Data aliases
14 bands = spin_data.bands
15 kpt_cart = spin_data.kpt_cart
16 if component == "x":
17 projection = spin_data.sigma_x
18 elif component == "y":
19 projection = spin_data.sigma_y
20 else:
21 projection = spin_data.sigma_z
22
23 # Evaluate k_len
24 k_len = np.zeros(kpt_cart.shape[0])
25 for i in range(1, kpt_cart.shape[0]):
26 dk = kpt_cart[i] - kpt_cart[i-1]
27 k_len[i] = k_len[i-1] + np.linalg.norm(dk)
28
29 # Plot fat band
30 for ib in range(bands.shape[1]):
31 plt.scatter(k_len, bands[:, ib], c=projection[:, ib], s=5.0, cmap="jet")
32 for x in k_len[k_idx]:
33 plt.axvline(x, color="k", linewidth=0.8, linestyle="-")
34 for y in (-2.0, -1.9):
35 plt.axhline(y, color="k", linewidth=1.0, linestyle=":")
36 plt.xlim(k_len[0], k_len[-1])
37 plt.xticks(k_len[k_idx], k_label)
38 plt.ylabel("Energy (t)")
39 plt.colorbar(label=fr"$\langle\sigma_{component}\rangle$")
40 plt.show()
The spin-resolved band structure for \(\sigma_z\) is shown in Fig. 2, which is consistent with Fig. 1, i.e., zero on \(\Gamma\)-\(M\) and non-zero on \(M\)-\(K\) paths.
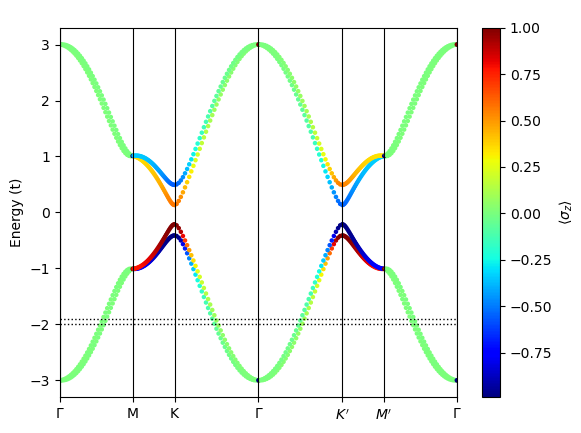
Spin-resolved band structure of Kane-Mele model. Horizontal dashed lines indicate the energy range for plotting spin texture in the right panel of Fig. 1.
Orbital order
The order of spin-polarized orbitals determines how the spin-up and spin-down components are extracted from the
eigenstates. There are two popular orders: spin-major and orbital-major. For example, there are two \(p_z\)
orbitals in the two-band model of monolayer graphene in the spin-unpolarized case, which can be denoted as
\(\{\phi_1, \phi_2\}\). When spin has been taken into consideration, the orbitals become
\(\{\phi_1^{\uparrow}, \phi_2^{\uparrow}, \phi_1^{\downarrow}, \phi_2^{\downarrow}\}\). In spin-major order
they are sorted as \([\phi_1^{\uparrow}, \phi_2^{\uparrow}, \phi_1^{\downarrow}, \phi_2^{\downarrow}]\),
while in orbital-major order they are sorted as
\([\phi_1^{\uparrow}, \phi_1^{\downarrow}, \phi_2^{\uparrow}, \phi_2^{\downarrow}]\). In the C++ backend
of SpinTexture class, the spin-up and spin-down components are extracted as:
1size_t num_orb_half = num_orbitals / 2;
2auto seq_up = Eigen::seq(0, num_orb_half - 1, 1);
3auto seq_down = Eigen::seq(num_orb_half, num_orbitals - 1, 1);
4if (!spin_major) {
5 seq_up = Eigen::seq(0, num_orbitals - 2, 2);
6 seq_down = Eigen::seq(1, num_orbitals - 1, 2);
7}
8// ...
9Eigen::VectorXcd spin_up(num_orb_half); // half size
10Eigen::VectorXcd spin_down(num_orb_half); // half size
11// ...
12spin_up = eigenstates(seq_up, ib);
13spin_down = eigenstates(seq_down, ib);
If the spin-polarized orbitals follow other user-defined orders, the users should modify the
SpinTexture::calc_spin_texture C++ function to correctly extract the spin-up and spin-down
components.