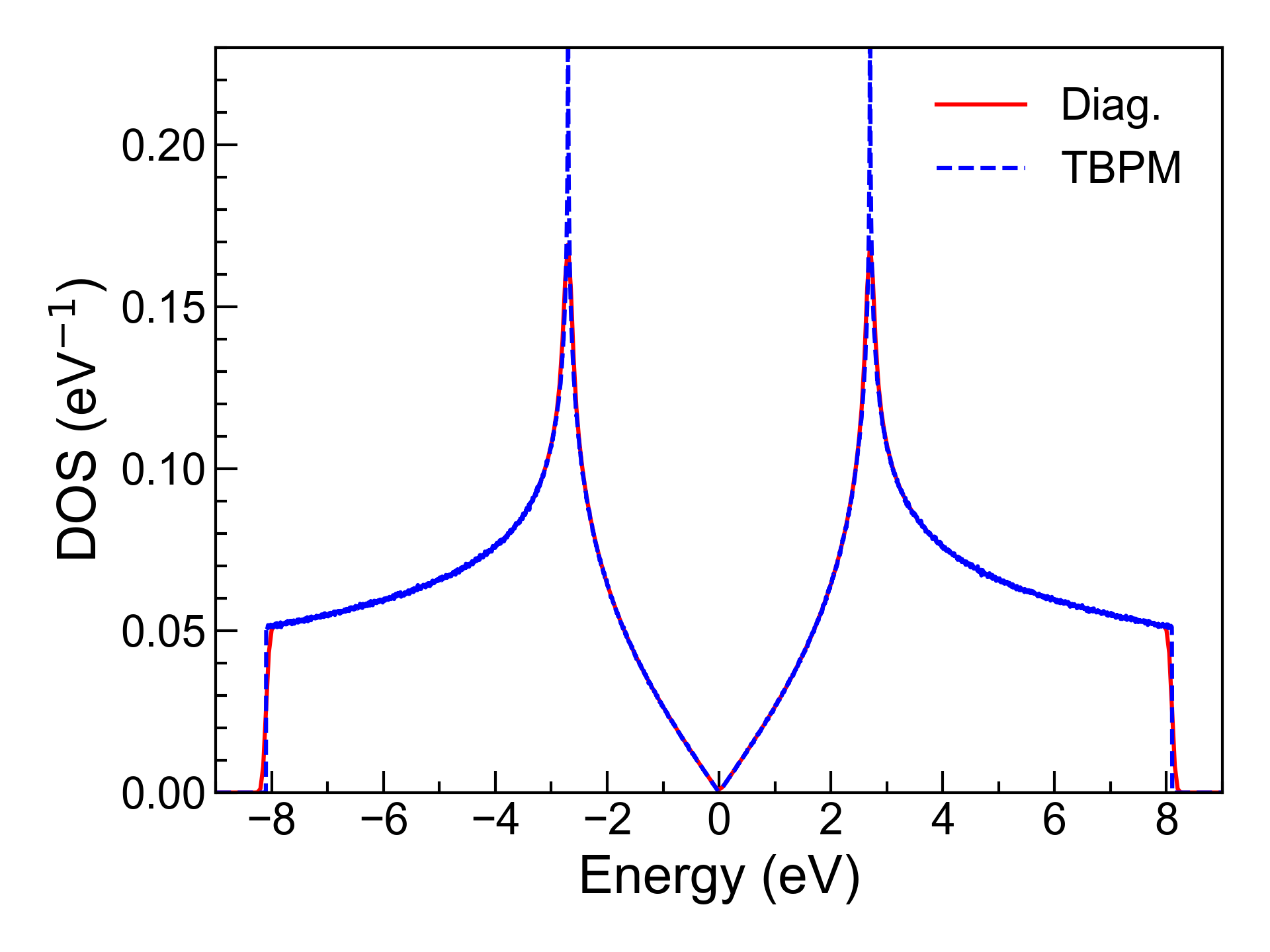
Band structure and DOS

In this tutorial, we show how to calculate the band structure and density of states (DOS) of a primitive cell using monolayer graphene as the example. The script can be found at examples/prim_cell/band_dos/graphene.py. First of all, we need to import all necessary packages:

import numpy as np
import matplotlib.pyplot as plt
import tbplas as tb

Of course, we can reuse the model built in Setting up the primitive cell. But this time we will import it from the materials repository for convenience:

cell = tb.make_graphene_diamond()

The first Brillouin zone of a hexagonal lattice with \(\gamma=60^\circ\) is shown as below:

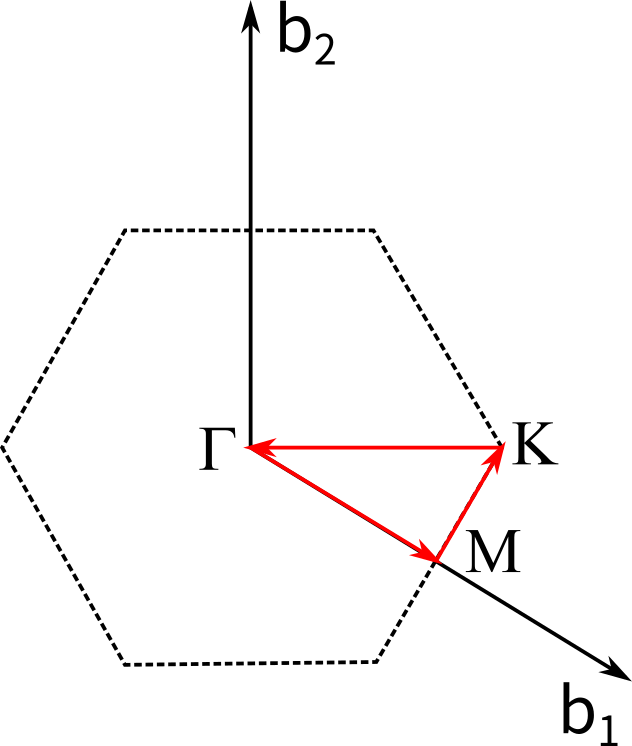
../../_images/FBZ.png

Schematic plot of the first Brillouin zone of a hexagonal lattice. \(b_1\) and \(b_2\) are basis vectors of reciprocal lattice. Dashed hexagon indicates the edges of first Brillouin zone. The path of \(\Gamma \rightarrow M \rightarrow K \rightarrow \Gamma\) is indicated with red arrows.

We generate a path of \(\Gamma \rightarrow M \rightarrow K \rightarrow \Gamma\), with 40 interpolated k-points along each segment, using the following commands:

k_points = np.array([
    [0.0, 0.0, 0.0],    # Gamma
    [1./2, 0.0, 0.0],   # M
    [2./3, 1./3, 0.0],  # K
    [0.0, 0.0, 0.0],    # Gamma
])
k_label = ["G", "M", "K", "G"]
k_path, k_idx = tb.gen_kpath(k_points, [40, 40, 40])

Here k_points is an array contaning the fractional coordinates of highly-symmetric k-points, which are then passed to gen_kpath() for interpolation. k_path is an array containing interpolated coordinates and k_idx contains the indices of highly-symmetric k-points in k_path. k_label is a list of strings to label the k-points in the plot of band structure.

The band structure can be obtained by:

k_len, bands = cell.calc_bands(k_path)

and plotted by calling the plot_bands() method of Visualizer class:

vis = tb.Visualizer()
vis.plot_bands(k_len, bands, k_idx, k_label)

or alternatively, using matplotlib directly:

num_bands = bands.shape[1]
for i in range(num_bands):
    plt.plot(k_len, bands[:, i], color="r", linewidth=1.0)
for idx in k_idx:
    plt.axvline(k_len[idx], color='k', linewidth=1.0)
plt.xlim((0, np.amax(k_len)))
plt.xticks(k_len[k_idx], k_label)
plt.xlabel("k (1/nm)")
plt.ylabel("Energy (eV)")
plt.tight_layout()
plt.show()
plt.close()
../../_images/bands.png

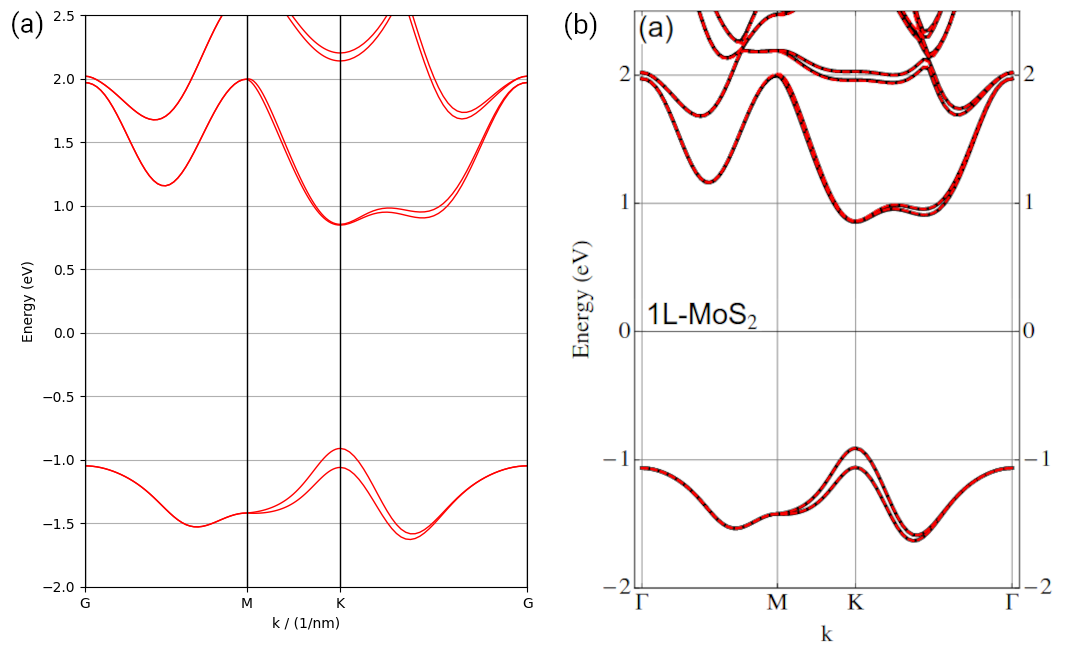
Band structure of monolayer graphene.

To evaluate density of states (DOS) we need to generate a uniform k-mesh in the first Brillouin zone using the gen_kmesh() function:

k_mesh = tb.gen_kmesh((120, 120, 1))  # 120*120*1 uniform meshgrid

Then we can calculate and visulize DOS with the calc_dos() method of Visualizer class:

energies, dos = cell.calc_dos(k_mesh)
vis.plot_dos(energies, dos)

Of course, we can also plot DOS using matplotlib directly:

plt.plot(energies, dos, linewidth=1.0)
plt.xlabel("Energy (eV)")
plt.ylabel("DOS (1/eV")
plt.tight_layout()
plt.show()
plt.close()
../../_images/dos.png