Quasi-crystal

In this tutorial, we show how to construct the quasi-crystal, in which we also need to shift twist, reshape and merge the cells. Taking bi-layer graphene quasi-crystal as an example, a quasi-crystal with 12-fold symmetry is formed by twisting one layer by \(30^\circ\) with respect to the center of \(\mathbf{c} = 2/3\ \mathbf{a}_1 + 2/3\ \mathbf{a}_2\), where \(\mathbf{a}_1\) and \(\mathbf{a}_2\) are the lattice vectors of the primitive cell of fixed layer. The script can be found at examples/advanced/quasi_crystal.py. We begin with importing the packages:

import math
from typing import Union, Tuple

import numpy as np
from numpy.linalg import norm

import tbplas as tb

The main function for constructing the quasi-crystal is defined as:

def main():
    prim_cell = tb.make_graphene_diamond()
    dim = (33, 33, 1)
    angle = 30 / 180 * math.pi
    center = np.array((2./3, 2./3, 0))
    radius = 3.0
    shift = 0.3
    cell = make_quasi_crystal_pc(prim_cell, dim=dim, angle=angle, center=center,
                                 radius=radius, shift=shift)
    cell.plot(with_cells=False, with_orbitals=False, hop_as_arrows=False,
              hop_eng_cutoff=0.3)

Firstly, we define the geometric parameters. We need a large cell to hold the quasi-crystal, whose dimension is given in dim. angle is the twisting angle and center is the fractional coordinate of twisting center. The radius of the quasi-crystal is controlled by radius, while shift specifies the interlayer distance. The function make_quasi_crystal_pc is defined as:

def make_quasi_crystal_pc(prim_cell: tb.PrimitiveCell,
                          dim: Tuple[int, int, int],
                          angle: float,
                          center: np.ndarray,
                          radius: float = 3.0,
                          shift: float = 0.3) -> tb.PrimitiveCell:
    """
    Create quasi-crystal at primitive level.

    :param prim_cell: primitive cell from which the quasi-crystal is built
    :param dim: dimension of the extended primitive cell
    :param angle: twisting angle in RADIAN
    :param center: fractional coordinate of the twisting center in the primitive cell
    :param radius: radius of quasi-crystal in nm
    :param shift: distance of shift along z-axis in NANOMETER
    :return: the quasi-crystal
    """
    # Get the Cartesian coordinate of rotation center
    center = np.array([dim[0]//2, dim[1]//2, 0]) + center
    center = np.matmul(center, prim_cell.lat_vec)

    # Build fixed and twisted layers
    layer_fixed = tb.extend_prim_cell(prim_cell, dim=dim)
    layer_twisted = tb.extend_prim_cell(prim_cell, dim=dim)

    # Rotate and shift twisted layer
    tb.spiral_prim_cell(layer_twisted, angle=angle, center=center,
                        shift=shift)

    # Remove unnecessary orbitals
    cutoff_pc(layer_fixed, center=center, radius=radius)
    cutoff_pc(layer_twisted, center=center, radius=radius)

    # Reset the lattice of twisted layer
    layer_twisted.reset_lattice(layer_fixed.lat_vec, layer_fixed.origin,
                                unit=tb.NM, fix_orb=True)

    # Build inter-cell hopping terms
    inter_hop = tb.PCInterHopping(layer_fixed, layer_twisted)
    neighbors = tb.find_neighbors(layer_fixed, layer_twisted,
                                  a_max=0, b_max=0, max_distance=0.75)
    for term in neighbors:
        i, j = term.pair
        inter_hop.add_hopping(term.rn, i, j, calc_hop(term.rij))

    # Extend hopping terms
    extend_hop(layer_fixed)
    extend_hop(layer_twisted)
    final_cell = tb.merge_prim_cell(layer_fixed, layer_twisted, inter_hop)
    return final_cell

where we firstly get the Cartesian coordinate of the twisting center, then build the fixed and twisted layers and twist the twisted layer with respect to the center, as is done in Build hetero-structure. The twisting operation is done by the spiral_prim_cell() function, where the Cartesian coordinate of the center is given in the center argument. Then we remove unnecessary orbitals to produce a round quasi-crystal with finite radius. This is done by calling the cutoff_pc function, which is defined as:

def cutoff_pc(prim_cell: tb.PrimitiveCell,
              center: np.ndarray,
              radius: float = 3.0) -> None:
    """
    Cutoff primitive cell up to given radius with respect to given center.

    :param prim_cell: supercell to cut
    :param center: Cartesian coordinate of center in nm
    :param radius: cutoff radius in nm
    :return: None. The incoming supercell is modified.
    """
    idx_remove = []
    orb_pos = prim_cell.orb_pos_nm
    for i, pos in enumerate(orb_pos):
        if norm(pos[:2] - center[:2]) > radius:
            idx_remove.append(i)
    prim_cell.remove_orbitals(idx_remove)
    prim_cell.trim()

where we loop over orbital positions to collect the indices of unnecessary orbitals, then call the remove_orbitals and trim functions. Before merging the fixed and twisted layers, we need to reset the lattice vectors and origin of twisted layer to that of fixed layer by calling the reset_lattice function. Then we can merge them safely by calling the merge_prim_cell() function. Finally, we extend the hoppings and visualize the quasi-crystal, where the extend_hop function is defined in Build hetero-structure. The output is shown in following figure:

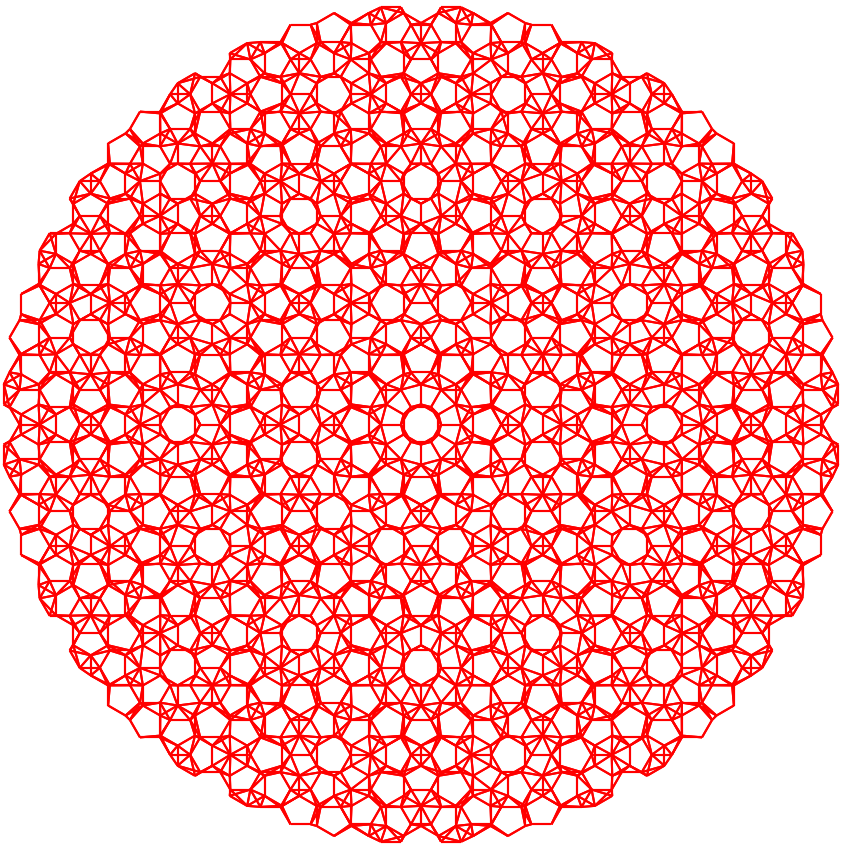
Plot of the quasi-crystal formed from the incommensurate \(30^\circ\) twisted bi-layer graphene with a radius of 3 nm.