Fractal
In this tutorial, we will take the Sierpiński carpet as an example and show the procedure of constructing fractals. Generally, fractals can be constructed in two approaches, namely bottom-up and top-down, as demonstrated in Fig. 1. The bottom-up approach builds the fractal by iteratively replicating the fractal of low iteration number following some specific pattern. On the contrary, the top-down approach builds a large model at first, then recursively removes unnecessary orbitals and hopping terms following the pattern. Both approaches can be implemented with TBPLaS, while the top-down approach is faster.
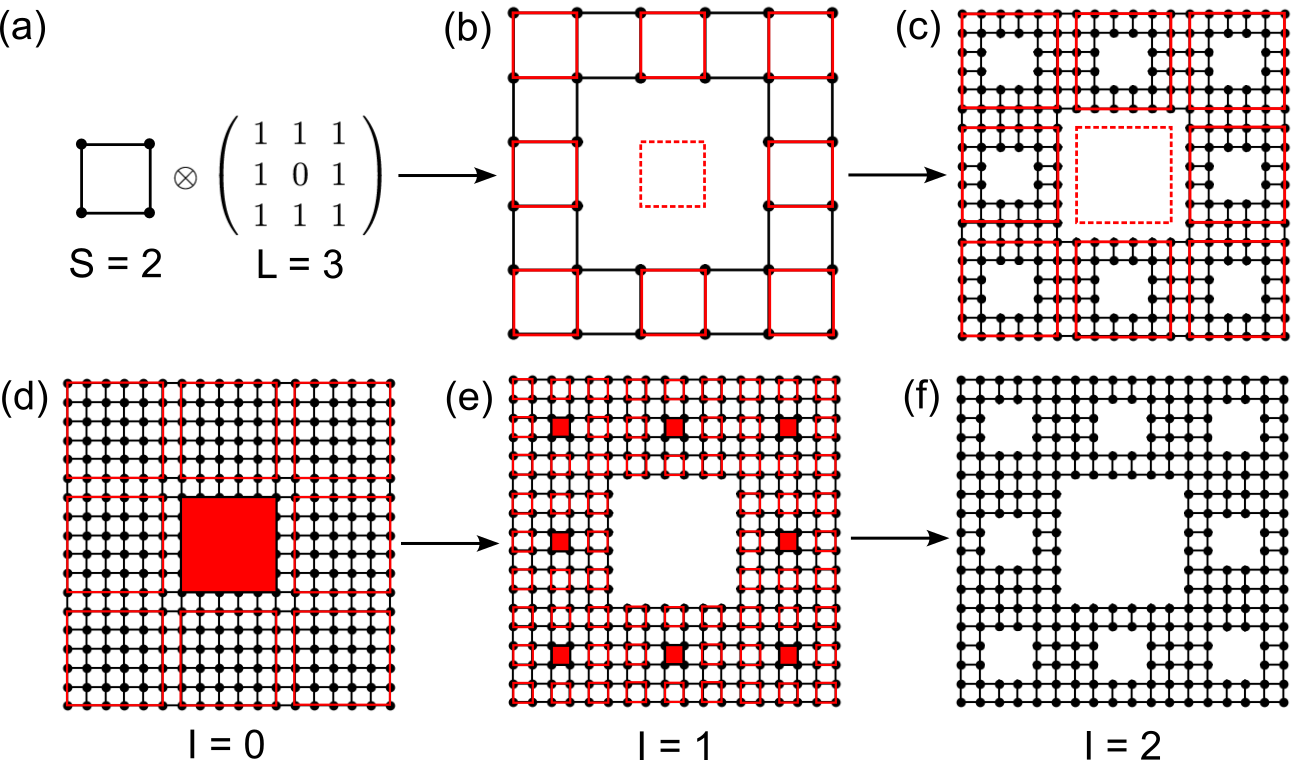
Schematic plot of constructing Sierpiński carpet with \(S=2\), \(L=3\) and \(I=2\) in (a)-(c) bottom-up and (d)-(f) top-down approaches. The dashed squares in (a)-(c) and filled squares in (d)-(f) indicate the void areas in the fractal.
The scripts of this tutorial are located at examples/advanced/fractal/prim_cell.py. We begin with
importing the necessary packages:
import numpy as np
import tbplas as tb
from mask import Box, Mask
Top-down approach
For the top-down approach, we also need to utilize the Box and Mask classes from the
mask module located at the same directory as the scripts.
The Box class represents a rectangular area spanning from \([i_0, j_0]\) to
\((i_1, j_1)\). If the box is marked as void, then the orbitals inside it will be removed.
The Mask class is a collection of boxes, which recursively partitions them into smaller boxes
and marks the central boxes as void. It offers the etch_prim_cell function to produce the
fractal by removing orbitals falling into void boxes at the PrimitiveCell level, and the
etch_super_cell at SuperCell level. In this tutorial, we will build the fractal at
PrimitiveCell level. The usage of etch_super_cell can be found in
examples/advanced/fractal/sample.py
We define the following function to build the fractal in top-down approach:
1def top_down(prim_cell: tb.PrimitiveCell, start_width: int,
2 iteration: int, extension: int) -> tb.PrimitiveCell:
3 """
4 Build fractal in top-down approach.
5
6 :param prim_cell: primitive cell of square lattice
7 :param start_width: starting width of the sample
8 :param iteration: iteration number of sample
9 :param extension: extension of the sample width
10 :return: fractal
11 """
12 # Create the extended cell
13 final_width = start_width * extension**iteration
14 extended_cell = tb.extend_prim_cell(prim_cell,
15 dim=(final_width, final_width, 1))
16 extended_cell.apply_pbc((False, False, False))
17
18 # Create the mask
19 start_box = Box(0, 0, final_width - 1, final_width - 1)
20 mask = Mask(start_box, num_grid=extension, num_iter=iteration)
21
22 # Remove orbitals
23 mask.etch_prim_cell(extended_cell, final_width)
24 return extended_cell
The Sierpiński carpet is characterized by 3 parameters: the starting width \(S\), the extension
\(L\) which controls the pattern, and the iteration number \(I\), as shown in Fig. 1. We
extend the square primitive cell to the final width of the carpet in line 13-16, which is
determined as \(D = S \cdot L^I\). Then we create a box covering the whole extended cell and a
mask from the box in line 19-20. The bottom-left corner of the box is located at \([0, 0]\),
while the top-right corner is at \((D-1, D-1)\). Then we call the etch_prim_cell function
to remove the orbitals falling into void boxes of the mask in line 23. Finally, the fractal is
returned.
Bottom-up approach
We define the following function to build the fractal in bottom-up approach:
1def bottom_up(prim_cell: tb.PrimitiveCell, start_width: int,
2 iteration: int, extension: int) -> tb.PrimitiveCell:
3 """
4 Build fractal in bottom-up approach.
5
6 :param prim_cell: primitive cell of square lattice
7 :param start_width: starting width of the sample
8 :param iteration: iteration number of sample
9 :param extension: extension of the sample width
10 :return: fractal
11 """
12 # Create the extended cell
13 final_width = start_width * extension**iteration
14 extended_cell = tb.extend_prim_cell(prim_cell,
15 dim=(final_width, final_width, 1))
16 extended_cell.apply_pbc((False, False, False))
17
18 # Build 0-th order fractal
19 fractal = [(ia, ib)
20 for ia in range(start_width)
21 for ib in range(start_width)]
22
23 # Build pattern for replication
24 pattern = [(ia, ib)
25 for ia in range(extension)
26 for ib in range(extension)
27 if not (1 <= ia < extension-1 and 1 <= ib < extension-1)]
28
29 # Build n-th order fractal by replicating (n-1)-th order according to
30 # pattern, which is a direct product mathematically
31 for i in range(iteration):
32 fractal_new = []
33 width = start_width * extension**i
34 for entry in pattern:
35 di = width * entry[0]
36 dj = width * entry[1]
37 replica = [(grid[0] + di, grid[1] + dj) for grid in fractal]
38 fractal_new.extend(replica)
39 fractal = fractal_new
40
41 # Get grid coordinates of vacancies
42 full_sites = [(ia, ib)
43 for ia in range(final_width)
44 for ib in range(final_width)]
45 vacancies = list(set(full_sites).difference(set(fractal)))
46 vacancies = [(grid[0], grid[1]) for grid in vacancies]
47
48 # Create the model
49 masked_id_pc = [i[0] * final_width + i[1] for i in vacancies]
50 masked_id_pc = sorted(masked_id_pc)
51 extended_cell.remove_orbitals(masked_id_pc)
52 return extended_cell
Similar to the top-down approach, we also need to extend the primitive cell in line 13-16. Then we
build the 0-th order of fractal and the replication pattern in line 19-27. After that, we replicate
the fractal according to the pattern iteratively to get the final fractal, which is a list of
tuples containing the grid coordinates of the reserved orbitals. Then we get the grid coordinates
of the orbitals to remove using set operations. Finally, the orbitals are removed by calling
remove_orbitals method of PrimitiveCell and the fractal is returned.
Build the model
We demonstrate the usage of top-down and bottom-up approaches by:
1def main():
2 # Create a square lattice
3 lattice = np.eye(3, dtype=np.float64)
4 prim_cell = tb.PrimitiveCell(lattice)
5 prim_cell.add_orbital((0, 0))
6 prim_cell.add_hopping((1, 0), 0, 0, 1.0)
7 prim_cell.add_hopping((0, 1), 0, 0, 1.0)
8 prim_cell.add_hopping((1, 1), 0, 0, 1.0)
9 prim_cell.add_hopping((1, -1), 0, 0, 1.0)
10
11 # Create fractal using top-down approach
12 fractal = top_down(prim_cell, 2, 3, 3)
13 fractal.plot(with_cells=False, with_orbitals=False, hop_as_arrows=False)
14
15 # Create fractal using bottom-up approach
16 fractal = bottom_up(prim_cell, 2, 3, 3)
17 fractal.plot(with_cells=False, with_orbitals=False, hop_as_arrows=False)
18
19
20if __name__ == "__main__":
21 main()
The output is shown in the following figure:

Sierpiński carpet with \(S=2\), \(L=3\) and \(I=3\).