Build hetero-structure

In this tutorial, we show how to build hetero-structure taking twisted bilayer graphene as the example. The workflow of constructing hetero structures is shown in Fig. 1(a). First of all, we determine the twisting angle and lattice vectors of the hetero-structure. Then we build the primitive cells of each layer, shift the twisted layer along \(z\)-axis by the interlayer distance and rotate it by the twisting angle. After that, we reshape the primitive cells to the lattice vectors of the hetero-structure to yield the layers, as depicted in Fig. 1(b). When all the layers are ready, we merge them into one cell and add the intralayer and interlayer hopping terms up to a given cutoff distance. For the visualization of Moiré pattern, we also need to build a sample from the merged cell. The script can be found at examples/advanced/tbg.py. Before constructing the model, we need to import the required packages:

import math

import numpy as np
from numpy.linalg import norm

import tbplas as tb

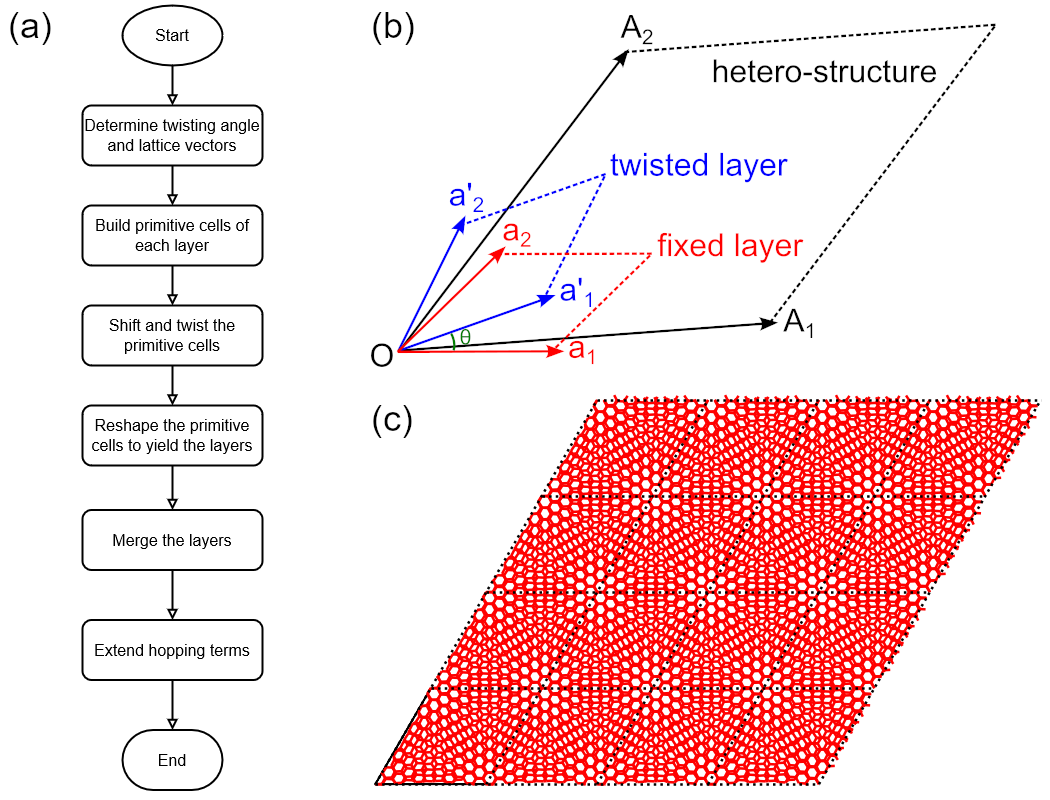
(a) Workflow of constructing hetero-structure. (b) Schematic plot of lattice vectors of fixed (\(\mathbf{a}_1\), \(\mathbf{a}_2\)) and twisted (\(\mathbf{a}_1^\prime\), \(\mathbf{a}_2^\prime\)) primitive cells and the hetero-structure (\(\mathbf{A}_1\), \(\mathbf{A}_2\)), as well as the twisting angle \(\theta\). (c) Twisted bilayer graphene sample with \(4\times4\times1\) merged cells of \(i=5\).

Auxiliary functions

The twisting angle and lattice vectors are determined following the formulation in ref1:

\[\begin{split}\theta_i &= \arccos \frac{3i^2+3i+1/2}{3i^2+3i+1} \\ \mathbf{A}_1 &= i\cdot\mathbf{a}_1 + (i+1)\cdot\mathbf{a}_2 \\ \mathbf{A}_2 &= -(i+1)\cdot\mathbf{a}_1 + (2i+1)\cdot\mathbf{a}_2\end{split}\]

where \(\mathbf{a}_1\) and \(\mathbf{a}_2\) are the lattice vectors of the primitive cell of fixed layer and \(i\) is the index of hetero-structure. We define the following functions accordingly:

def calc_twist_angle(i: int) -> float:
    """
    Calculate twisting angle according to the reference.

    :param i: parameter controlling the twisting angle
    :return: twisting angle in RADIANs, NOT degrees
    """
    cos_ang = (3 * i ** 2 + 3 * i + 0.5) / (3 * i ** 2 + 3 * i + 1)
    return math.acos(cos_ang)


def calc_hetero_lattice(i: int, prim_cell_fixed: tb.PrimitiveCell) -> np.ndarray:
    """
    Calculate Cartesian coordinates of lattice vectors of hetero-structure
    according to the reference.

    :param i: parameter controlling the twisting angle
    :param prim_cell_fixed: primitive cell of fixed layer
    :return: (3, 3) float64 array, Cartesian coordinates of hetero-structure
        lattice vectors in NANOMETER
    """
    hetero_lattice = np.array([[i, i + 1, 0],
                               [-(i + 1), 2 * i + 1, 0],
                               [0, 0, 1]])
    hetero_lattice = tb.frac2cart(prim_cell_fixed.lat_vec, hetero_lattice)
    return hetero_lattice

calc_twist_angle returns the twisting angle in radians, while calc_hetero_lattice returns the Cartesian coordinates of lattce vectors in nm. After merging the layers, we need to add the interlayer hopping terms. Meanwhile, the intralayer hoppings terms should also be extended in the same approach. We define the extend_hop function to achieve these goals:

def extend_hop(prim_cell: tb.PrimitiveCell, max_distance: float = 0.75) -> None:
    """
    Extend the hopping terms in primitive cell up to cutoff distance.

    :param prim_cell: primitive cell to extend
    :param max_distance: cutoff distance in NM
    :return: None. Incoming primitive cell is modified
    """
    neighbors = tb.find_neighbors(prim_cell, a_max=1, b_max=1,
                                  max_distance=max_distance)
    for term in neighbors:
        i, j = term.pair
        prim_cell.add_hopping(term.rn, i, j, calc_hop(term.rij))

Here we call the find_neighbors function to get the neighboring orbital pairs up to the cutoff distance max_distance. Then the hopping terms are evaluated according to the displacement vector rij with the calc_hop function and added to the primitive cell. The calc_hop function is defined according to the formulation in ref2:

def calc_hop(rij: np.ndarray) -> float:
    """
    Calculate hopping parameter according to Slater-Koster relation.
    See ref. [2] for the formulae.

    :param rij: (3,) array, displacement vector between two orbitals in NM
    :return: hopping parameter in eV
    """
    a0 = 0.1418
    a1 = 0.3349
    r_c = 0.6140
    l_c = 0.0265
    gamma0 = 2.7
    gamma1 = 0.48
    decay = 22.18
    q_pi = decay * a0
    q_sigma = decay * a1
    dr = norm(rij).item()
    n = rij.item(2) / dr
    v_pp_pi = - gamma0 * math.exp(q_pi * (1 - dr / a0))
    v_pp_sigma = gamma1 * math.exp(q_sigma * (1 - dr / a1))
    fc = 1 / (1 + math.exp((dr - r_c) / l_c))
    hop = (n**2 * v_pp_sigma + (1 - n**2) * v_pp_pi) * fc
    return hop

Build the model

With all the functions ready, we proceed to build the hetero-structure. Firstly, we evaluate the twisting angle of bilayer graphene for \(i=5\). Then we construct the primitive cells of the fixed and twisted layers with the make_graphene_diamond() function. The fixed primitive cell is located at \(z=0\) and does not need rotation or shifting. On the other hand, the twisted primitive cell needs to be rotated counter-clockwise by the twisting angle and shifted towards \(+z\) by 0.3349 nm, which is done with the spiral_prim_cell() function. After that, we reshape the primitive cells to the lattice vectors of hetero-structure with the make_hetero_layer() function, which is a wrapper to coordinate conversion and reshape_prim_cell(). Then the layers are merged with merge_prim_cell() and the hopping terms are extended with extend_hop using a cutoff distance of 0.75 nm. Finally, a sample with \(4\times4\times1`\) merged cells is created and plotted, with the hopping terms below 0.3 eV hidden for clarity. The output is shown in Fig. 1(c), where the Moiré pattern can be clearly observed.

def main():
    # Evaluate twisting angle
    i = 5
    angle = calc_twist_angle(i)

    # Prepare primitive cells of fixed and twisted layer
    prim_cell_fixed = tb.make_graphene_diamond()
    prim_cell_twisted = tb.make_graphene_diamond()

    # Shift and rotate the twisted layer
    tb.spiral_prim_cell(prim_cell_twisted, angle=angle, shift=0.3349)

    # Reshape primitive cells to the lattice vectors of hetero-structure
    hetero_lattice = calc_hetero_lattice(i, prim_cell_fixed)
    layer_fixed = tb.make_hetero_layer(prim_cell_fixed, hetero_lattice)
    layer_twisted = tb.make_hetero_layer(prim_cell_twisted, hetero_lattice)

    # Merge layers
    merged_cell = tb.merge_prim_cell(layer_fixed, layer_twisted)

    # Extend hopping terms
    extend_hop(merged_cell, max_distance=0.75)

    # Visualize Moire pattern
    sample = tb.Sample(tb.SuperCell(merged_cell, dim=(4, 4, 1), pbc=(True, True, False)))
    sample.plot(with_orbitals=False, hop_as_arrows=False, hop_eng_cutoff=0.3)


if __name__ == "__main__":
    main()