Response functions

In this tutorial, we show how to calculate the response functions of primitive cell, namely dynamic polarization, dielectric function and optical (AC) conductivity, using the Lindhard class. The corresonding script is examples/prim_cell/lindhard.py. Lindhard requires the energies and wave functions from exact diagonalization, so its application is limited to primitive cells of small or moderate size. For large models, the tight-binding propagation method (TBPM) is recommended, which will be discussed in Properties from TBPM. Before beginning the tutorial, we import all necessary packages and create a graphene primitive cell as the example:

import numpy as np
import matplotlib.pyplot as plt
import tbplas as tb

# Make graphene primitive cell
t = 3.0
vectors = tb.gen_lattice_vectors(a=0.246, b=0.246, c=1.0, gamma=60)
cell = tb.PrimitiveCell(vectors, unit=tb.NM)
cell.add_orbital([0.0, 0.0], label="C_pz")
cell.add_orbital([1 / 3., 1 / 3.], label="C_pz")
cell.add_hopping([0, 0], 0, 1, t)
cell.add_hopping([1, 0], 1, 0, t)
cell.add_hopping([0, 1], 1, 0, t)

Create a Lindhard object

A Lindhard object can be created by:

# Create a Lindhard object
lind = tb.Lindhard(cell=cell, energy_max=10, energy_step=1000,
                   kmesh_size=(600, 600, 1), mu=0.0, temperature=300, g_s=2,
                   back_epsilon=1.0, dimension=2)

Here cell is the primitive cell we have just created. energy_max and energy_step specify an energy grid on which the response functions will be evaluated. k_mesh specifies a k-grid in the first Brillouin zone. mu is the chemical potential in eV. temperature is in Kelvin. g_s is spin-degeneracy. back_epsilon is the relative dielectric constant of background. Since graphene is two-dimensional, we turn on 2-d specific algorithms by setting dimension to 2.

Dynamic polarization

Lindhard class offers two methods to calculate the dynamic polarization: calc_dyn_pol_regular() and calc_dyn_pol_arbitrary(). Both methods require an array of q-points. The difference is that calc_dyn_pol_arbitrary() accepts arbitrary q-points as input, while calc_dyn_pol_regular() requires that the q-points should be on the k-grid defined by k_mesh. This can be explained from the equation for polarization:

\[\Pi(\textbf{q},\omega)=\frac{g_s}{(2\pi)^n}\int_{\mathrm{BZ}}\mathrm{d}^n\textbf{k}\sum_{l,l^\prime}\frac{n_\mathrm{F}(E_{\textbf{k}l})-n_\mathrm{F}(E_{\textbf{k}^{\prime}l^{\prime}})}{E_{\textbf{k}l}-E_{\textbf{k}^{\prime}l^{\prime}}+\hbar\omega+\mathrm{i}\eta^+}|\langle\textbf{k}^{\prime}l^{\prime}|\mathrm{e^{\mathrm{i}\textbf{q}\cdot\textbf{r}}|\textbf{k}l\rangle}|^2\]

where \(\textbf{k}^{\prime} = \textbf{k} + \textbf{q}\). For any regular q-point on the k-grid, \(\textbf{k}^{\prime}\) is still on the same k-grid. However, this may not be true for arbitrary q-points. So, calc_dyn_pol_arbitrary() keeps two sets of energies and wave functions, for \(\textbf{k}\) and \(\textbf{k} + \textbf{q}\) grids respectively, although they may be equivalent via translational symmetry. On the other hand, calc_dyn_pol_regular() takes translational symmetry into consideration and reuses energies and wave functions as much as possible. So, calc_dyn_pol_regular() uses less computational resources, at the price that only regular q-points on k-grid can be dealt with. As an example, the dynamic polarization of q-point with grid coordiante of \((20, 20, 0)\) on a \((600, 600, 1)\) kgrid can be evaluated as:

# Create a timer
timer = tb.Timer()

# Calculate dynamic polarization with calc_dyn_pol_regular
q_grid = np.array([[20, 20, 0]])
timer.tic("regular")
omegas, dp_reg = lind.calc_dyn_pol_regular(q_grid)
timer.toc("regular")
plt.plot(omegas, dp_reg[0].imag, color="red", label="Regular")
plt.legend()
plt.show()
plt.close()

Note that we have put additional code into the example for benchmarking purposes. The output is shown in the left panel of the figure:

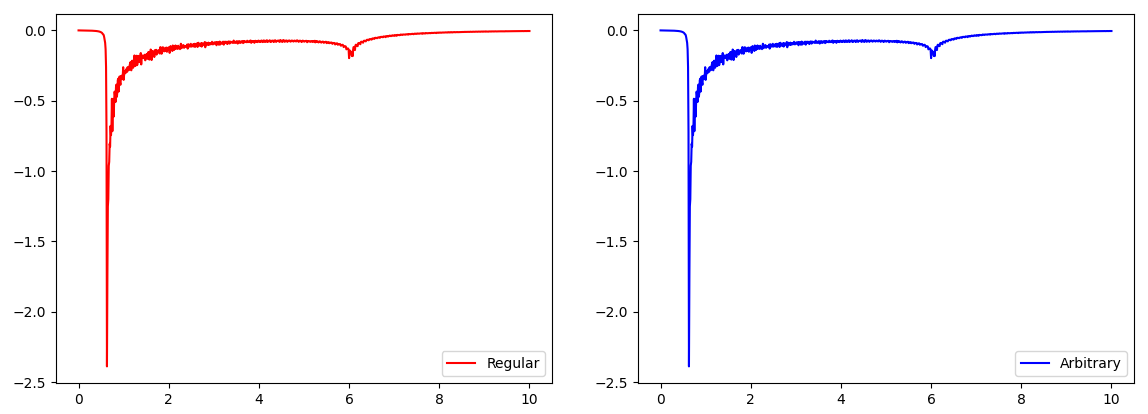
../../_images/dp.png — Dynamic polarization from calc_dyn_pol_regular and calc_dyn_pol_arbitrary.

Unlike calc_dyn_pol_regular() which accepts grid coordinates as input, calc_dyn_pol_arbitrary() requires the Cartesian coordinates of q-points in nanometer. A method grid2cart() has been provided for converting the coordinates. The dynamic polarization of the same q-point can be also evaluated by calc_dyn_pol_arbitrary() as:

# Calculate dynamic polarization with calc_dyn_pol_arbitrary
q_cart = lind.grid2cart(q_grid, unit=tb.NM)
timer.tic("arbitrary")
omegas, dp_arb = lind.calc_dyn_pol_arbitrary(q_cart)
timer.toc("arbitrary")
plt.plot(omegas, dp_arb[0].imag, color="blue", label="Arbitrary")
plt.legend()
plt.show()
plt.close()

timer.report_total_time()

The output is shown in the right panel of the figure above. Obviously, both methods give the same resutls. But calc_dyn_pol_arbitrary() takes almost twice the time:

  regular :       5.61s
arbitrary :       9.74s

Dielectric function

The dielectric function is determined from the dynamic polarization via:

\[\epsilon(\textbf{q},\omega)=1-V(\textbf{q})\Pi(\textbf{q},\omega)\]

and implemented in the calc_epsilon() method. As a more realistic example, the dielectric function of \(|q|=4.76 nm^{-1}\) and \(\theta = 30^\circ\) can be evaluated as:

# Reproduce the result of Phys. Rev. B 84, 035439 (2011) with
# |q| = 4.76 / nm and theta = 30 degrees.
lind = tb.Lindhard(cell=cell, energy_max=18, energy_step=1800,
                   kmesh_size=(1200, 1200, 1), mu=0.0, temperature=300, g_s=1,
                   back_epsilon=1.0, dimension=2)
q_points = 4.76 * np.array([[0.86602540, 0.5, 0.0]])
omegas, dyn_pol = lind.calc_dyn_pol_arbitrary(q_points)
epsilon = lind.calc_epsilon(q_points, dyn_pol)
plt.plot(omegas, epsilon[0].real, color="red")
plt.xticks(np.linspace(0.0, 18.0, 10))
plt.show()
plt.close()

The output is shown in the left panel of the figure below, as well as the reference taken from Phys. Rev. B 84, 035439 (2011).

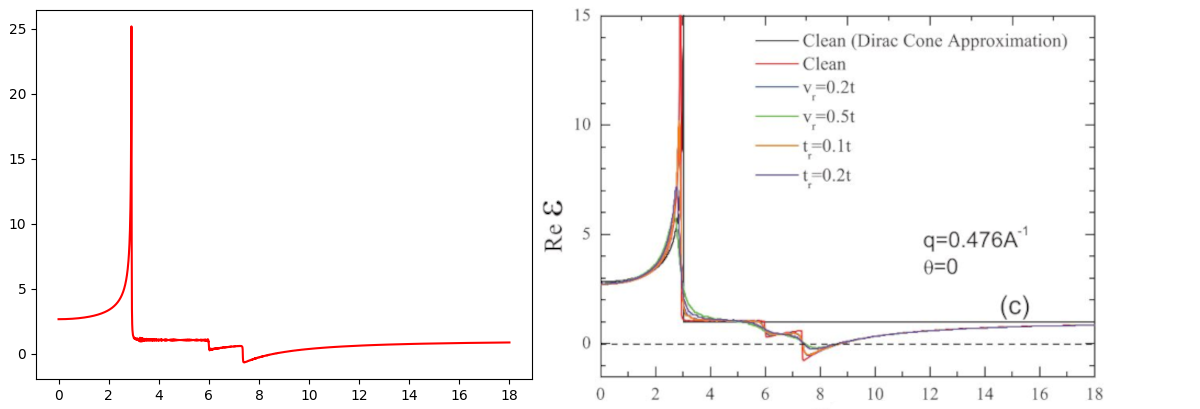
../../_images/epsilon.png — Dielectric function of \(|q|=4.76 nm^{-1}\) and \(\theta = 30^\circ\)

AC conductivity

The AC conductivity is evaluated through the Kubo-Greewoord formula:

\[\sigma_{\alpha\beta}(\omega)=\frac{\mathrm{i} e^2 \hbar}{N_k \Omega_c}\sum_{\textbf k}\sum_{n,m} \frac{f_{m\textbf{k}} - f_{n\textbf{k}}}{\epsilon_{m\textbf{k}} - \epsilon_{n\textbf{k}}} \frac{\langle\psi_{n\textbf k}|v_\alpha|\psi_{m\textbf k}\rangle \langle\psi_{m\textbf k}|v_\beta|\psi_{n\textbf k}\rangle}{\epsilon_{m\textbf{k}} - \epsilon_{n\textbf{k}}-(\hbar\omega+\mathrm i\eta^+)}\]

and implemented in the calc_ac_cond() method. As AC conductivity is not q-dependet, no q-points are required as input. We demonstrate the usage of this method by calculating the AC conductivity of monolayer graphene by:

# Reproduce the result of Phys. Rev. B 82, 115448 (2010).
lind = tb.Lindhard(cell=cell, energy_max=t*3.5, energy_step=2048,
                   kmesh_size=(2048, 2048, 1), mu=0.0, temperature=300.0,
                   g_s=2, back_epsilon=1.0, dimension=2)
omegas, ac_cond = lind.calc_ac_cond()
omegas /= t
ac_cond *= 4
plt.plot(omegas, ac_cond.real, color="red")
plt.minorticks_on()
plt.show()
plt.close()

The result is shown in the left of the figure below, as well as the reference taken from Phys. Rev. B 82, 115448 (2010).

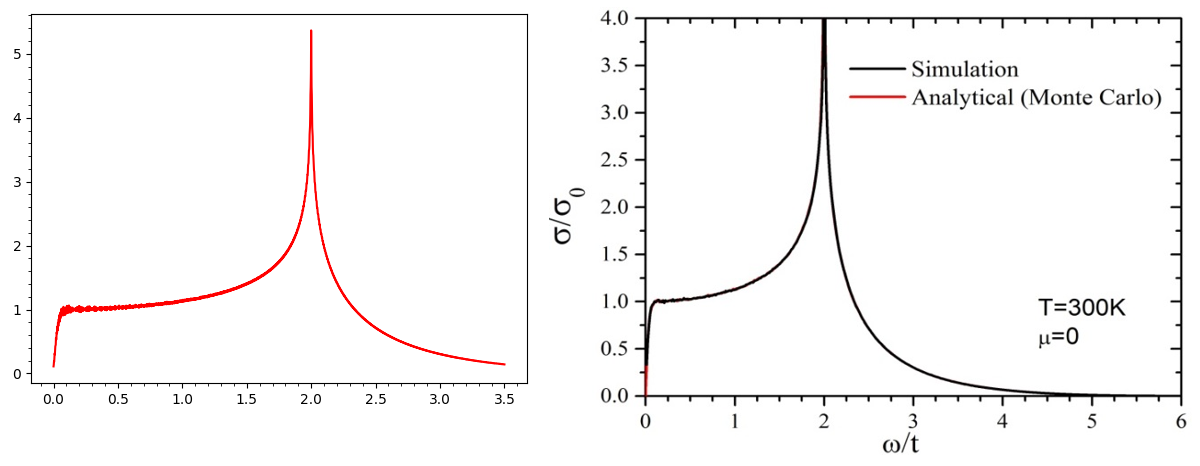
../../_images/ac_cond.png — AC conductivity of monolayer graphene.

Notes on system dimension

Lindhard class deals with system dimension in two approaches. The first approach is to treat all systems as 3-dimensional. In this approach, supercell technique is required, with vacuum layers added on non-periodic directions. Also, the component(s) of kmesh_size should be set to 1 accordingly on that direction. The seond approach utilizes dimension-specific formula whenever possible. For now, only 2-dimensional case has been implemented. This approach requires that the system should be periodic in xOy plane, i.e. the non-periodic direction should be along \(c\) axis.

Regarding the accuracy of results, the first approach suffers from the issue that dynamic polarization and AC conductivity scale inversely proportional to the product of supercell lengths, i.e., \(|c|\) in 2d case and \(|a|*|b|\) in 1d case. This is caused by elementary volume in reciprocal space (\(\mathrm{d}^{3}k\)) in Lindhard function. On the contrary, the second approach has no such issue. If the supercell lengths of non-periodic directions are set to 1 nm, then the first approach yields the same results as the second approach.

For the dielectric function, the situation is more complicated. From the equation for epsilon we can see that it is also affected by the Coulomb potential \(V(q)\), which is \(V(q)=\frac{1}{\epsilon_0\epsilon_r}\cdot\frac{4\pi e^2}{q^2}\) in 3-d case and \(V(q)=\frac{1}{\epsilon_0\epsilon_r}\cdot\frac{2\pi e^2}{q}\) in 2-d case, respectively. So the influence of system dimension is q-dependent. Setting supercell length to 1 nm will NOT reproduce the same result as the second approach.